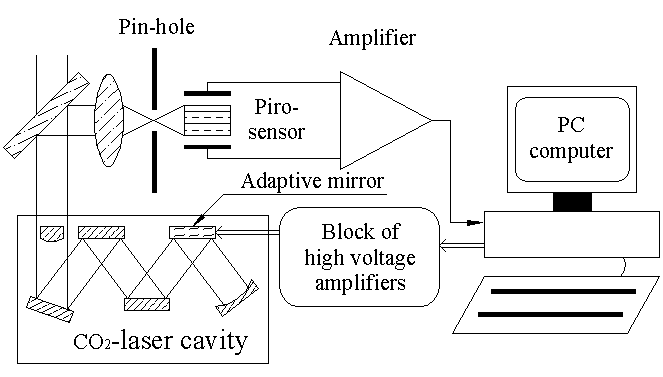
Fig.1. One of the possible designs of an adaptive system for the intracavity laser beam control
The possible design of an active system of laser beam formation and control is presented on Fig.1.

Here adaptive corrector in placed inside the laser cavity of a multypath CO2 laser. As a sensor a simple pin-hole with a piro-sensor and amplifier is used. And the system of control consists of a computer and the block of high voltage amplifiers. While designing the adaptive system the main problem is to choose the appropriate corrector - the key element of any adaptive system, that might be used to control the laser beam. Table 1 gives the amplitude and the frequency range of the typical average aberrations that were detected inside the cavities of the industrial CO2 and YAG:Nd3+ lasers. As it was seen from the table, these aberrations are mostly low-order ones, and rather slow (up to 30 Hz).
| Type of laser | Type of aberrations | Amplitude (P-V) of this aberrations | Frequency range |
|---|---|---|---|
| Solid state YAG (output power 150 W) | Astigmatism
Coma Spherical ab. | 8 μ
2 μ 5 μ | Up to 30 Hz |
| CO2 industrial laser (output power 1 kW) | Defocus
Astigmatism Coma | 10 μ
4 μ 4 μ | Up to 3 Hz |
So, when deciding what kind of active corrector would be most suitable for the intracavity laser beam control we should first of all keep in mind the necessity to compensate for these low-order aberrations and to use the less number channels to correct them. In fact that means that we have to use the corrector with the so called modal response functions of actuators. And among these type of deformable mirrors the most appropriate ones are the bimorph semipassive correctors16,17, 18.
The traditional semipassive bimorph mirror consists of a glass, copper or quartz substrate firmly glued to a plate actuator disk made from piezoelectric ceramic (lead zirconium titanate, PZT) (see Fig.2).
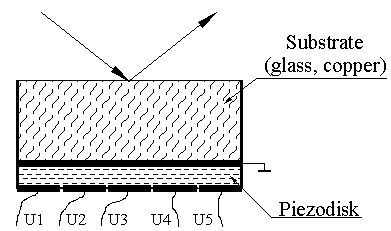
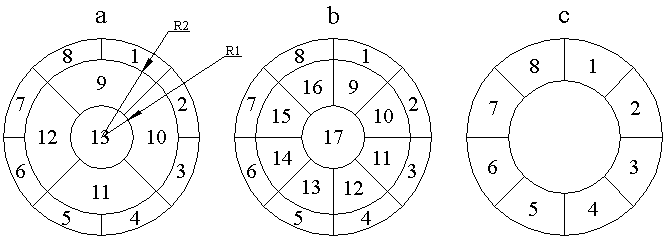
Applying the electrical signal to the electrodes of the piezoceramic plate causes, for example, tension of the piezodisc. Glued substrate prevents this tension, and this results in the deformation of the reflective surface. To reproduce different types of aberrations with the help of such corrector the outer electrode is divided in several controlling electrodes, that have the shape of a part of a sector. The size as well as the number of such electrodes depends upon the number and the type of the aberrations to be corrected. In our work we usually used the geometry of the electrodes given on Fig. 3.
The behavior of the bimorph corrector (deformation of the surface when the voltage is applied to the particular electrode) is well described by the following equation19:
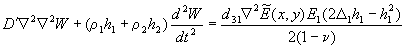 ;
;
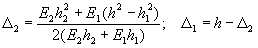 ;
;
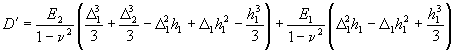 .
.
Here, h1, h2 - the thickness of a piezodisk, and
substrate, E1, E2 - Young's modulus of a piezodisk and
substrate, h - total thickness of the mirror, ν - the Poisson ratios, d31 -
transverse piezo modulus, 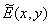 - the strength of the electric field
applied uniformly to the given electrode.
- the strength of the electric field
applied uniformly to the given electrode.
This equation was used to optimise radii R1 and R2 (Fig. 3) for the best correction of the low order aberrations such as coma, astigmatism, spherical aberration.
Several types of the bimorph correctors were produced in the Group of the Adaptive Optics in the Scientific Research Center for Technological Lasers Russian Academy of Sciences. The technology of fabrication of such a corrector was the following: semipassive bimorph plate was heated in a furnace for 4 - 5 h at 80° C until the glue had completely hardened. The plate was then cooled in a refrigerator to remove any residual thermal deformations before being reheated in the furnace. This procedure was repeated four or five times. The quartz substrate was then polished to obtain an optical-quality surface (the deviation from sphere should not be greater then 0.1 μ) before a high reflectivity dielectric of metal coating (up to 99.98%) was deposited on its surface. Conductors were then glued to the common and controlled electrodes. The corrector was inserted in a mounting at the back of which there was a connection to the control voltages. The main features of a semipassive bimorph corrector are shown in table 2.
| Working aperture | 40, 50 mm |
| Thickness of the mirror | 3 - 5 mm |
| Number of actuators | 8, 13, 18 |
| Mirror quality | 0.2 μ (P-V) |
| Stroke | 7 - 15 μ |
| First resonance | 2 - 7 kHz |
| Substrate material | Glass, quartz, copper |
The static and dynamic characteristics of the mirrors were studied by an interference method. We used Zygo Mark-3 phase-shifting interferometer. The sensitivity of correctors was estimated from the displacement of the interference fringes at the center of the pattern when the voltage of 100 V was applied to all electrodes. It amounted to 1.7 μ. The frequency of the first resonance of our correctors was in the range of 3 - 5 kHz. The response functions of the middle ring of electrodes of the 13-element corrector are presented in Fig. 4.
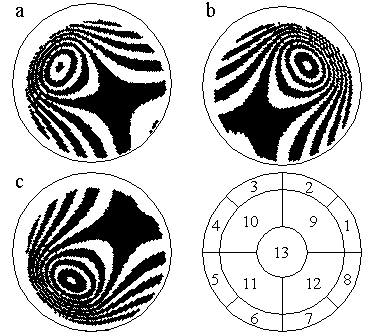
It should be pointed out that the response functions of every electrode of this corrector is the modal one, meaning that by applying voltage to a given element we get the deformation of the whole mirror surface. This result on the one hand complicates the process of mirror control but at the same time reduces the number of elements that need to be used to correct for the low-order aberrations. Analyzing the level map given in Fig. 4 we can point out that the shape of the response functions of different electrodes looks very close, and the amplitude of the surface deformation is also very close.
Table 3 presents the measured RMS errors of approximation of some low-order aberrations by 17-electrode bimorph corrector.
| Type of aberration | RMS error |
|---|---|
| Defocus | 0.1 % |
| Astigmatism | 0.2 % |
| Coma | 3.0 % |
| Spherical aberration | 5.3 % |
As it is shown in 2.1, a plane controlled semipassive bimorph mirror can efficiently reproduce any second-order aberration. But one of the problems of such types of mirrors is the rather high thermal deformation of the reflecting surface of the corrector. Such a sensitivity could exceed 0.5μ/°C, and depends strongly on the difference between coefficients of the thermal deformations of the material of the substrate and piezoceramics. This effect limits the possible field of application of the bimorph correctors. That is why it is necessary to eliminate any undesirable heating of the adaptive mirror by radiation accompanied by an uncontrolled deformation of the corrector surface. One way is to substitute a piezoplate with a ring of piezoceramics. So, laser beam will not be absorbed by piezomaterial.
Also, for some applications it is desirable to use not the flat, but concave or convex active corrector. Thus, we worked out a circular concave semipassive bimorph mirror with piezoceramics actuating ring (Fig. 5).
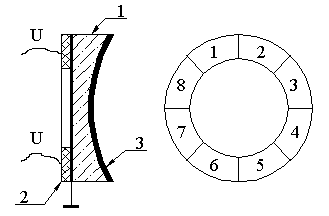
Eight control electrodes were evaporated to the outside of the ring while a common grounded electrode was deposited to the inside.
The operating principle of the corrector was the same as that of a plane mirror, but the response functions of individual electrodes should differ from those of a plane mirror. This was because the thickness of the mirror decreased almost 1.5 times from the edge toward the center for the given 600 mm radius of curvature. The response functions of the corrector were measured using a modified Fizeau interferometer and the interferograms were analyzed using IBM computer20. Fig. 6 shows the response functions of first three electrodes when a control voltage -150 V was applied to them.
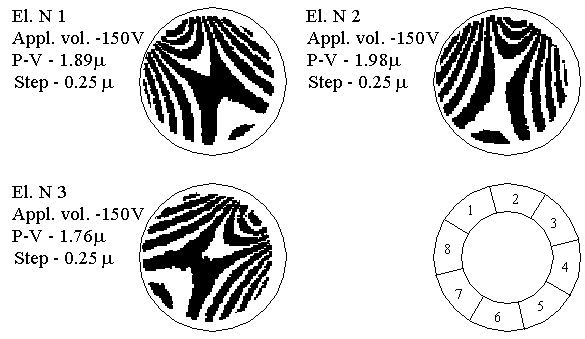
The astigmatic deformation of the surface is clearly visible. The largest deviation was found near the drive mechanism. Table 4 gives the coefficients of expansion Ai of the response functions of the first, second and third electrodes in terms of the Zernike polynomials. It can be seen that in contrast to a flat bimorph mirror19, the coefficients A9, A10, A16 and A17 play a significant role. The amplitude of the shift of the corrector at the center when a voltage of 300 V was applied to all the control electrodes was 6 μ.
| N | A3 | A4 | A5 | A6 | A7 | A9 | A10 | A16 | A17 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0,18 | 0,34 | 0,62 | -0,03 | 0,04 | -0,31 | -0,03 | 0,10 | -0,14 |
| 2 | 0,19 | 0,69 | -0,24 | 0,03 | 0,05 | 0,17 | 0,28 | -0,14 | 0,11 |
| 3 | 0,19 | -0,11 | -0,70 | 0,01 | 0,05 | 0,12 | -0,28 | 0,16 | -0,06 |
Here by definition we have: N - electrode number, A3=2r2-1, A4=r2 cos2θ, A5=r2 sin2θ, A6=(3r2 -2)r cosθ , A7=(3r2-2)r sinθ, A9 =r3 cos3θ , A10=r3 sin3θ, A16=r4 cos4θ, A17=r4 sin4θ, where r and θ are polar coordinates (coefficients are given in microns).
Radiation from a CW solid-state laser at a wavelength of 1.064 mm was directed to this adaptive mirror. Interferometric measurements showed that at power densities up to 100 W/cm2 there was no deformation of the corrector surface.
For high average power CO2 lasers there is the problem of constructing controllable cooled mirrors, production of which is rather complicated. A corrector of this kind should satisfy a number of technical requirements: it should have the necessary optical strength, its service life should be long (~ 1000 hours), and it should be easy to construct and use. The mirror surface should be continuously deformable and the amplitude of displacement of the corrector surface should be ~λ/2 (λ=10.6 μ - is the wavelength of the corrected radiation).
In NICTL we have developed water cooled mirrors based on semi-passive bimorph piezoelement. They consisted of a copper (or molybdenum) plate 2.5 mm thick and 100 mm in diameter. One side of the plate was polished and used as a mirror, whereas two piezoelectric ceramic disks 0.3 mm thick and 50 and 46 mm in diameter were glued on the other side (Fig. 7).
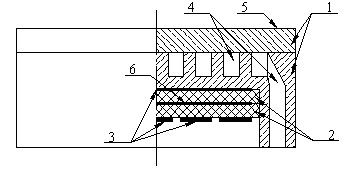
First piezodisk was used to control for the curvature of the mirror surface and 17 electrodes (Fig. 3) were evaporated on the outer side of the second piezodisk to compensate for different aberrations of the wavefront. The cooling system of the corrector was of the waffle type. A copper plate consisted of two solded disks in which channels of 0.5 mm deep were formed for the circulation of the cooling liquid. The size of the contact areas between the plates was 3x3 mm.
The static and dynamic characteristics of the mirror were determined by an interference method. The sensitivity of correctors was estimated from the displacement of the interference fringes at the center of the pattern when the voltage of 100 V was applied to all electrodes. It amounted to 1,7 μ. The frequency of first resonance of our correctors was in the range of 3 - 4 kHz. An active mirror was tested under an optical load of CO2 laser radiation with an average power density of 2.5 kW/cm² 21. The corrector surface profile was determined using a shearing interferometer. This optical load produced practically no deformation of the mirror surface, indicating that the cooling system was effective. The rate of flow of cooling water was 400 mliter/min. There were no distortions of corrector response function under the action of this load. A similar test of an uncooled adaptive mirror resulted in considerable thermal deformation of the surface.