
Fig.1. Typical view of the Hartmann pattern
Shack-Hartmann wavefront sensor (SHWS) was designed to measure both intensity distribution and phase distortion of optical fields in real time and high accuracy. It can be widely used not only in measuring, diagnostic, but also in adaptive optical systems to compensate for phase distortions. Various parameters such as peak-to-valley, root-mean square, Zernike coefficients, beam quality (M2) could be calculated with the help of such a sensor. The results of wavefront measurements by using our SHWS are reported in this paper.
Keywords: wavefront aberrations, Shack-Hartmann wavefront sensor, least-squares solution, Zernike polynomials expansion, beam quality factor M2 (M-square).
The adaptive optical systems became widely used in laser technology, microtechnology, laser ophthalmology, astronomical devices, optical communications and etc. For the measurements and testing of the aberrations of wavefront the adaptive optical systems include WaveFront sensor1-7.
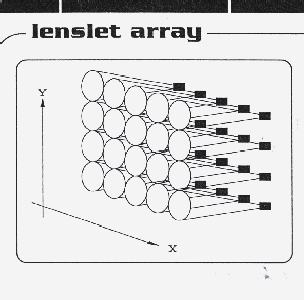
One of the most well known and widely used Shack-Hartmann sensor estimates the wavefront local slopes and consists of a lenslet array and a CCD camera. The centroids of sub-images fabricated by each lens of lenslet are determined and the sensor output is a set of {x, y} spot positions. The SHWS has some advantages for wavefront measuring of a laser beam with a large aperture. Noise properties of this sensor are well determined. It is simple to operate such a sensor. This resulted in the fact that SHWS became the most popular wavefront sensor for adaptive optics1,2.
Generally, the wavefront estimation procedure may be categorized as either zonal or modal, depending on whether the phase is presented like a number of local slopes of the wavefronts or in terms of coefficients of some modal functions determined on the whole aperture. In this paper we introduce a modal algorithm. Here we use Zernike polynomials as modal functions and least squares method to obtain the coefficients.
The Shack Hartmann wavefront sensor divides wavefront surface into a number of beamlets by a two-dimensional sub-apertures of the lenslet array. Each sub-aperture provides a separate focus on the detector of a CCD camera. The position of each spot is displaced by local wavefront aberrations. Thus, the periodical structure of the spots is the initial object for following investigations to be made by computer program. This picture is named the Hartman pattern (Fig. 1).


Wavefront measurement by SHWS is based on the measurements local slopes of a distorted
wavefront 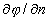 relative to a reference plane
wavefront. The local slope is proportional to the displacement of the spot
center ΔS. Fig.2 shows schematically the SHWS principle.
relative to a reference plane
wavefront. The local slope is proportional to the displacement of the spot
center ΔS. Fig.2 shows schematically the SHWS principle.
The displacement of the spot center xij c, yij c
within the sub-aperture with respect to a reference position xij r,
yij r is measured. Local gradient of the wavefront f(x,y) was obtained according
to 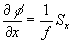 ,
, 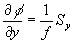 , where Sx=xc-xr,
, Sy= yc-yr, f is the focal length of the lenslets.
, where Sx=xc-xr,
, Sy= yc-yr, f is the focal length of the lenslets.
On the other hand the displacements could be represented in terms of Zernike polynomials:
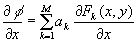 ,
, 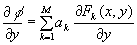 ,
,
where Fk(x,y) - two-dimensional orthogonal Zernike polynomials, M – number expansion coefficients ak.
In matrix form it could be written:
S=Aa
where A is so-called gradient rectangular matrix with M columns and 2NxNy rows (Nx - number of focal spots along x direction and Ny - along y direction).
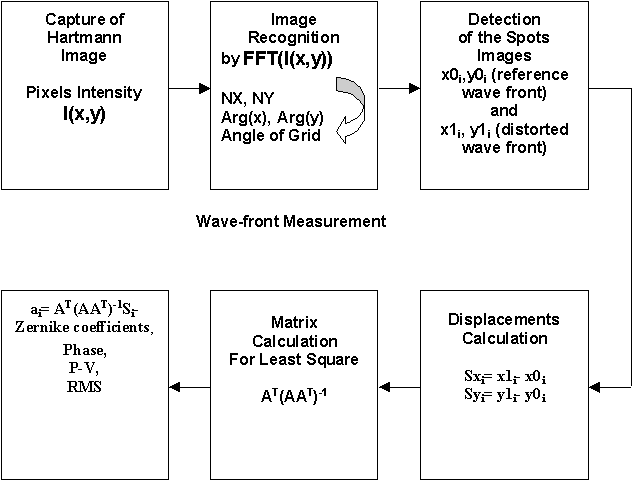
It is necessary to note, the Fast Fourier Transform was applied to the light periodical distribution of the spots image for determination the Nx and Ny grid parameters and for obtained the borders of this grid respect to the CCD matrix boundaries.
The position (x,y) of an image spot in each small region of the grid is determined by the centroid:
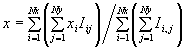 ,
, 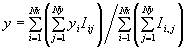 .
.
To find the model surface we used least square method:
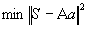 .
.
As a result we obtain Zernike coefficients:
a=BS, where B=(ATA)-1AT.
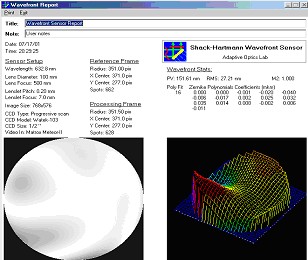
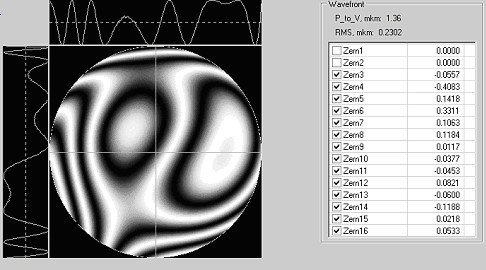
Now, when Zernike coefficients are obtained a level map of the surface is created in a number of equally spaced points, and it is displayed on the screen. All Zernike coefficients have a clear physical sense like tilt, focus, astigmatism, coma. Some of them are presented in the table. The RMS and peak-to-valley (P-V) - the difference between the highest and lowest points, could be easily calculated.
| Term | Name | Function |
|---|---|---|
| 1 | Tilt in X direction | X |
| 2 | Tilt in Y direction | Y |
| 3 | Focus | -1 + 2(x2+y2) |
| 4 | Astigmatism with axis at 0 (90) | y2-x2 |
| 5 | Astigmatism with axis at 45 | 2xy |
| 6 | Third order coma along x axis | -2x+3xy2+3x3 |
| 7 | Third order coma along y axis | -2y+3y3+3x2y |
| Up to 36 number | ||
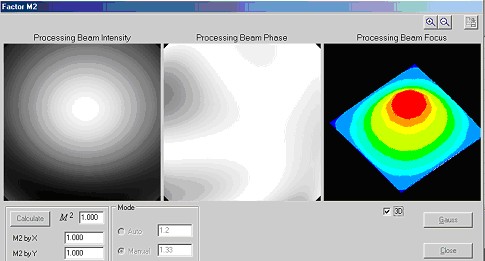
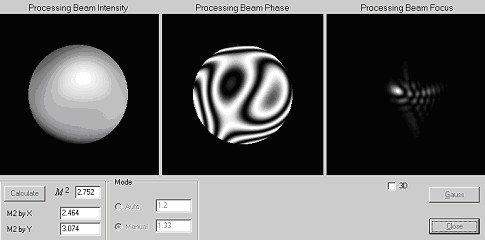
When the phase f(x,y) and the amplitude I(x,y) of the beam are obtained it is possible to calculate a M2 beam parameter. For the calculation we use simple Fourier transform algorithm:
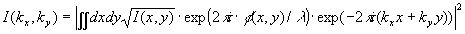 ,
,
where 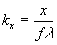 ,
, 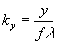 .
.
Beam quality factor M2 is calculated by the relationship given in the international standard ISO/DIS 11146 and could be defined by means of two values: the diameter of the beam in the near field d0 and the divergence angle θ:
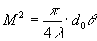 ,
,
where λ is the wavelength in the medium.
The divergence angle θ is defined
by the equation 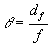 , where df is the beam diameter
in the focal plane of a lens with focus f. The diameters of a beam are defined
as second moments according the formulas are given in ISO/DIS 11146.
, where df is the beam diameter
in the focal plane of a lens with focus f. The diameters of a beam are defined
as second moments according the formulas are given in ISO/DIS 11146.
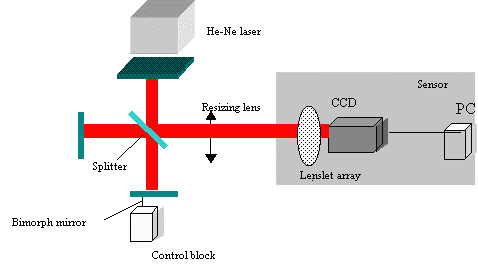
The Experimental Setup for laser beam diagnostic in laboratory is shown on Fig.3. A He-Ne laser is used as a light source. The aberrations are produced by bimorph mirror 1 in this laboratory setup. The mirror is controlled by control block 2. The beam of He-Ne laser 3 is reflected by mirror 1 and divided by the splitter 4. The lens 5 is matched for converting the beam aperture to the aperture of a CCD matrix 6. The laser beam divided into a number of beams by two-dimensional microlens arrays (lenslet, fl=7 mm, dl=0.22 mm) 7. Location of each spot was detected by a CCD camera and processed by a personal Pentium computer 8. Zygo interferometer 9 was included for testing of contour of phase, as this scheme allows to observe phase map by interferometer screen and SHWS simultaneously.
Maximal phase tilt taking into account diffraction radius of the spots produced by each lenslet could be estimated by the formula:
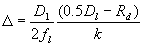 ,
,
here D1 is the diameter of beam on CCD, Dl is sub-aperture diameter;
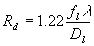 - diffraction beam radius,
- diffraction beam radius, 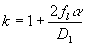 is scaling
coefficient,
is scaling
coefficient, 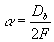 , Db – beam diameter, fl
– focus of resizing lens. For He-Ne laser Δ is about 10μm. Sensitivity of phase
determination is 0.06μm for the resolution of each lenslet spot position determination 0.5 pixel.
, Db – beam diameter, fl
– focus of resizing lens. For He-Ne laser Δ is about 10μm. Sensitivity of phase
determination is 0.06μm for the resolution of each lenslet spot position determination 0.5 pixel.
The sensor was used in practice for measuring the bimorph mirror response functions7-9 and investigation the regions, where they are linear relative to applied voltage. The voltages are applied to each electrode and Zernike coefficients are stored into computer memory. Some examples of such measurements with SHWS are represented below (Fig. 5). The measurements of bimorph mirror were used to test the linearity of the response functions of different electrodes (Fig.6).






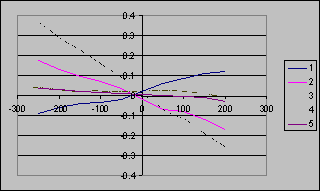
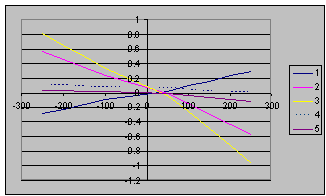
Sensor was used also to measure the wavefront in TiSp laser. (Max-Planck Institute for Quantum Optic, Laser-Plasma-Group, Garching, Gemany). Initial parameters of laser were - laser pulse energies 0.2 – 1.5 J; pulse duration’s 100 fs; frequency – 10 Hz. Example of wavefront measurement at pulse energies 200μJ is given bellow (Fig. 7, 8).
Low-cost, high precision wavefront sensor for wavefronts analyses was developed.
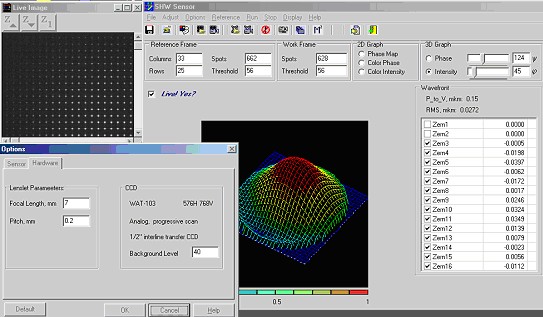
Hardware includes: lenslet array(Dl=0.2mm, fl=7mm); CCD camera Watec WAT-6, progressive scan, interline transfer ½’’ with 752x582 (CCIR); Matrox framegrabber Meteor II Standart ; Pentium II computer. Software was realized on C++ Builder 4. The example of user interface is represented in Fig.9. Sensor provides the measurements at real time up to 15 Hz. The maximal time of complete processing by optimum algorithm is 28 ms. The mathematical modeling of low order wavefront aberrations with their following analyze by computer code was realised. Obtained Zernike coefficients gave a good agreement with predetermined ones. The accuracy of phase reconstruction was better them 0.7 % for S/N ratio 10%. The limited angle of hartmannogramm rotation was 0.05 rad. The applied image recognition method to initial hartmanogramm made possible to obtain the geometry spots and the hartmanogramm arrangement relative to the boundary of CCD camera matrix. It simplified the initial analyze of hartmanogramm. The duration of the calibration stage was 1 s.